How to Solve “efficientRoadNetwork” in CodeFights

The Problem:

Once upon a time, in a kingdom far, far away, there lived a king Byteasar III. As a smart and educated ruler, he did everything in his (unlimited) power to make every single system of his kingdom efficient. The king went down in history as a great road builder: during his reign a great number of roads were built, and the road system he created was the most efficient for those dark times.

When you started to learn about Byteasar’s III deeds in your history classes, the creeping doubt crawled into the back of your mind: what if the famous king wasn’t so great after all? According to the most recent studies, there were n cities in the Byteasar’s kingdom, which were connected by the two-ways roads. You managed to get information about this roads from the university library, so now you can write a function that will determine whether the road system in Byteasar’s kingdom was efficient or not.

A road system is considered efficient if it is possible to travel from any city to any other city by traversing at most 2 roads.

Example

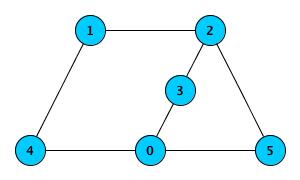
• For n = 6 and

  roads = [[3, 0], [0, 4], [5, 0], [2, 1],
            [1, 4], [2, 3], [5, 2]]
  

  the output should be

  efficientRoadNetwork(n, roads) = true.

  Here’s how the road system can be represented:

  

• For n = 6 and

  roads = [[0, 4], [5, 0], [2, 1],
            [1, 4], [2, 3], [5, 2]]
  

  the output should be

  efficientRoadNetwork(n, roads) = false.

  Here’s how the road system can be represented:

  

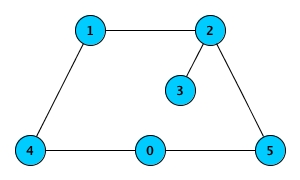
  As you can see, it’s only possible to travel from city 3 to city 4 by traversing at least 3 roads.

Input/Output

• [time limit] 7000ms (py)

• [input] integer nThe number of cities in the kingdom.

  Constraints:

  1 ≤ n ≤ 250.

• [input] array.array.integer roadsArray of roads in the kingdom. Each road is given as a pair [cityi, cityj], where 0 ≤ cityi, cityj < n and cityi ≠cityj. It is guaranteed that no road is given twice.

  Constraints:

  0 ≤ roads.length ≤ 35000,

  roads[i].length = 2,

  0 ≤ roads[i][j] < n.

• [output] booleantrue if the road system is efficient, false otherwise.

The Solution:

The Explanation:

Basic graph knowledge. (Adjacency Matrix)

The rows are the sources of the edges. Columns are the targets.

If we have a road from x to y; we have a road from y to x. (Since roads are to both directions.)

If there is no road between two cities, the adj cell for those two will be zero infinity, but since we will check if it is shorter than 2 or not, we can just put any number bigger than 2. I put 4.

update the roads as we iterate over the roads array.

update path from each node to itself. We can say the length from each node to itself is zero.

I used floyd-warshall all-pairs-shortest-path algorithm since the limits on number of nodes is small and it’s easy to implement. (Complexity of this algorithm is high, so, with higher number of nodes, we would have to use a more efficient algorithm.)

Check if all the roads are shorter than 3, if not return False.

else, return True.

How to Solve “roadsBuilding” in CodeFights

The Problem:

Once upon a time, in a kingdom far, far away, there lived a king Byteasar II. There was nothing special neither about him, nor about his kingdom. As a mediocre ruler, he did nothing about his kingdom and preferred hunting and feasting over doing anything about his kingdom prosperity.

Luckily, his adviser, wise magician Bitlin, was working for the kingdom welfare daily and nightly. However, since there was no one to advise him, he completely forgot about one important thing: the roads. Over the years most of the two-way roads built by Byteasar II predecessors were forgotten and no longer traversable. Only a few roads can still be used.

Bitlin wanted each pair of cities to be connected, but couldn’t find a way to figure out which roads are missing. Desperate, he turned to his magic crystal, seeking help. The crystal showed him a programmer from the distant future: you! Now you’re the only one who can save the kingdom. Given the existing roads and the number of cities in the kingdom, you should use the most modern technologies and find out what roads should be built again to make each pair of cities connected. Since the magic crystal is quite old and meticulous, it will only transfer the information that is sorted properly.

The roads to be built should be returned in an array sorted lexicographically, with each road stored as [cityi, cityj], where cityi < cityj.

How to Solve “newRoadSystem” in CodeFights

The Problem:

Once upon a time, in a kingdom far, far away, there lived a king Byteasar I. As a kind and wise ruler, he did everything in his (unlimited) power to make life of his subjects comfortable and pleasant. One cold evening a messenger arrived to the king’s castle with the latest news: all kings in the Kingdoms Union started to enforce traffic laws! In order not to lose his membership in the Union, king Byteasar had to do the same in his kingdom. But what would the citizens think of it?

The king decided to start introducing the changes with something more or less simple: change all the roads in the kingdom from two-directional to one-directional. He personally prepared the roadRegister of the new roads, and now he needs to make sure that the road system is convenient and there will be no traffic jams, i.e. each city has the same number of incoming and outgoing roads. As the Hand of the King, you’re the one who should check it.

Reminder

Please do inform me in case of a broken link in any content.