How to solve ‘trapRooms’ in CodeFights

~ waxtap

The Problem:

A zoological museum can be represented as a matrix in which each cell is a room. The alarm system in the museum allows visitors to go from each room only in one direction, specific to that room.

One night the exhibits went mad and messed the alarm system up. Now there are traps in the museum. A room is considered to be a trap if it’s impossible to leave the museum starting from it. A person leaves the building once he leaves the rectangle that represents it.

Given the museum’s configuration, find the number of traps in it.

Example

For

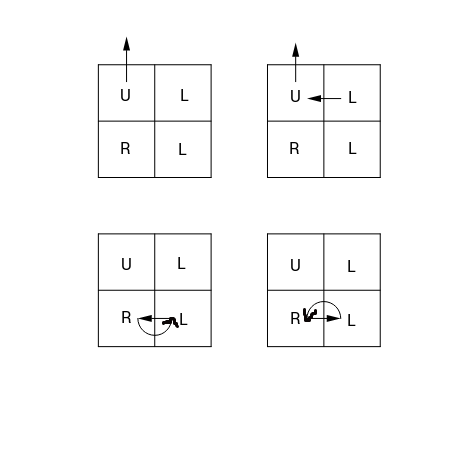
museum = [['U', 'L'],
          ['R', 'L']]

the output should be
trapRooms(museum) = 2.

There is no exit if you start from either of the bottom rooms.

Check out the image below for better understanding:

Input/Output

  • [time limit] 4000ms (py)
  • [input] array.array.char museum

    A non-empty rectangular matrix. The possible values of museum[i] are:

    • 'L' if it’s possible to move to the left;
    • 'R' if it’s possible to move to the right;
    • 'U' if it’s possible to move up;
    • 'D' if it’s possible to move down.

    Guaranteed constraints:
    1 ≤ museum.length ≤ 10,
    1 ≤ museum[0].length ≤ 10.

  • [output] integer

    The number of traps.

The Solution:

def trapRooms(museum):
    x=[[0]*len(museum[0]) for x in range(len(museum))]
    def rec(a,b,x):
        if not(a<len(museum) and a>=0 and b<len(museum[0]) and b>=0):
            return 0
        if x[a][b]:
            return 1
        s=0
        x[a][b]=1
        if museum[a][b]=='U':
            s+=rec(a-1,b,x)
        if museum[a][b]=='D':
            s+=rec(a+1,b,x)
        if museum[a][b]=='L':
            s+=rec(a,b-1,x)
        if museum[a][b]=='R':
            s+=rec(a,b+1,x)
        x[a][b]=0
        return s
    p=0
    for a in range(len(museum)):
        for b in range(len(museum[0])):
            p +=rec(a,b,x)
            print p
    return p

The Explanation:

We need to traverse the maze starting from each o the rooms and see if we can go outside, or go back to one of the rooms we have already passed. If we see any rooms we have already passed, that means we are stuck in the maze because the same room will always cause us to go back to same route.

 

 

Leave a comment