How to solve ‘trapRooms’ in CodeFights

The Problem:

A zoological museum can be represented as a matrix in which each cell is a room. The alarm system in the museum allows visitors to go from each room only in one direction, specific to that room.

One night the exhibits went mad and messed the alarm system up. Now there are traps in the museum. A room is considered to be a trap if it’s impossible to leave the museum starting from it. A person leaves the building once he leaves the rectangle that represents it.

Given the museum’s configuration, find the number of traps in it.

Example

For

museum = [['U', 'L'],
          ['R', 'L']]

the output should be
trapRooms(museum) = 2.

There is no exit if you start from either of the bottom rooms.

Check out the image below for better understanding:

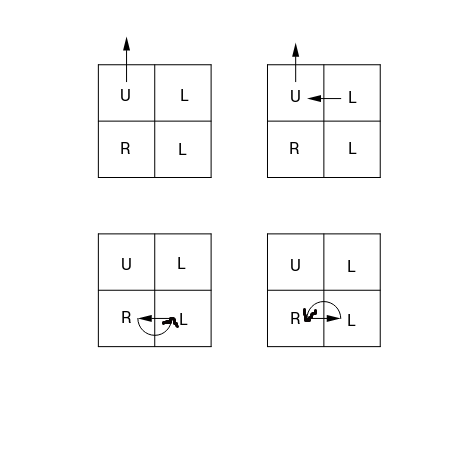
Input/Output

• [time limit] 4000ms (py)

• [input] array.array.char museum

  A non-empty rectangular matrix. The possible values of museum[i] are:

  • 'L' if it’s possible to move to the left;
  • 'R' if it’s possible to move to the right;
  • 'U' if it’s possible to move up;
  • 'D' if it’s possible to move down.

  Guaranteed constraints:
  1 ≤ museum.length ≤ 10,
  1 ≤ museum[0].length ≤ 10.

• [output] integer

  The number of traps.

The Solution:

def trapRooms(museum):
    x=[[0]*len(museum[0]) for x in range(len(museum))]
    def rec(a,b,x):
        if not(a<len(museum) and a>=0 and b<len(museum[0]) and b>=0):
            return 0
        if x[a][b]:
            return 1
        s=0
        x[a][b]=1
        if museum[a][b]=='U':
            s+=rec(a-1,b,x)
        if museum[a][b]=='D':
            s+=rec(a+1,b,x)
        if museum[a][b]=='L':
            s+=rec(a,b-1,x)
        if museum[a][b]=='R':
            s+=rec(a,b+1,x)
        x[a][b]=0
        return s
    p=0
    for a in range(len(museum)):
        for b in range(len(museum[0])):
            p +=rec(a,b,x)
            print p
    return p

The Explanation:

We need to traverse the maze starting from each o the rooms and see if we can go outside, or go back to one of the rooms we have already passed. If we see any rooms we have already passed, that means we are stuck in the maze because the same room will always cause us to go back to same route.

 

 

How to solve ‘bijectiveBase10’ in CodeFights

The Problem:

Consider a numeral system similar to base-10 numeral system with the only difference that it does not use a digit to represent zero; instead it has a digit to represent ten, such as A. It is called bijective base-10 system. For example, numbers that do not contain zeros in base-10 system remain the same when converted to bijective base-10 system.

Given a positive integer in base-10 system, return its representation in bijective base-10 system.

Example

• For a = 12345, the output should be
  bijectiveBase10(a) = "12345";
• For a = 10, the output should be
  bijectiveBase10(a) = "A";
• For a = 100, the output should be
  bijectiveBase10(a) = "9A".

  100 = 10 * 9 + 10 -> "9A".

• For a = 2010, the output should be
  bijectiveBase10(a) = "19AA".

  2010 = 1 * 103 + 9 * 102 + 10 * 10 + 10 -> "19AA".

Input/Output

• [time limit] 4000ms (py)

• [input] integer a

  A positive integer.

  Guaranteed constraints:
  10 ≤ a ≤ 6 · 108.

• [output] string

  The string representation of a in bijective base-10 system.

 

The Solution:

def bijectiveBase10(a):
    if '0' not in `a`:
        return `a`
    r=""
    while a>0:
        if a%10==0:
            a-=10
            r+="A"
        else:
            r+=str(a%10)
        a/=10
    return r[::-1]

The Explanation:

We need to understand the arithmetic behind this. For every 0 digit we see, we replace it with an ‘A’, which is 10. So, we decrease 10 from our number, because it is not zero anymore, but a ten. Then, we continue doing this just as if we are converting the number to another base. At the end, we have the reverse of the number, so, we return reverse.

The first if statement is actually unnecessary, it would work exactly the same without that if block.

How to solve ‘studentsAge’ in CodeFights

The Problem:

My friend Albi is a teacher. At the beginning of each lesson, her students form a line and enter the class one by one. As they enter, each student shakes her hand. Albi enters the students’ names in a list in the order in which they enter the classroom. After work, she analyzes the list to get a hint of the connections and relationships in the class.

Albi has a hunch that the ages of the students can tell her a lot. She has a list of the ages of her students in the order they entered the classroom, and she wants to calculate the number of pairs of students such that their age difference is exactly 1, and the youngest student in the pair entered before the oldest. Please help my friend!

Example

• For students = [2, 4, 3, 4, 6], the output should be
  studentsAge(students) = 2.

  There are two pairs of students Albi would be interested in: (2, 3) and (3, 4).

• For students = [5, 4, 9, 10], the output should be
  studentsAge(students) = 1.

  The only interesting pair of students in (9, 10).

Input/Output

• [time limit] 4000ms (py)

• [input] array.integer students

  The ages of the students in the order they entered the classroom.

  Guaranteed constraints:
  1 ≤ students.length ≤ 105,
  0 ≤ students[i] ≤ 105.

• [output] integer

  An integer with the answer for Albi.

The Solution:

def studentsAge(s):
    m=[0]*5**9
    c=0
    for x in s:
        c+=m[x-1]
        m[x]+=1
    return c

The Explanation:

There are multiple ways to solve this problem. Smarter way is to use a dictionary and store how many times each element is seen. However, to achieve the shortest solution (62 character in Python), we need a less efficient approach. Instead of a dictionary, create an array of size 10^5 and use this array to count each element.

For each element x in array, we need how many times x-1 is seen before that. So, for each element, we sum up this number and return it. The reason the array is initialized with length 5^9 is to decrease 1 character from 10^6.

How to Solve ‘Chemicals’ in CodeFights

The Problem:

Abby is a researcher at a company that makes chemical solutions. Her boss left her with a difficult task late Friday afternoon, and waltzed off into the weekend.

Abby has a hazardous liquid that reacts with oxygen by exploding. Her task is to distribute the liquid between special containers. The company buys containers of specific sizes in bulk, so she has access to a lot of containers of each size.

Since the liquid is explosive, Abby needs to fill the containers full to the exact capacity. Preparing the containers is tricky, so Abby wants to use as few containers as possible. Given the totalAmount of liquid and the set of container sizes containers, find the total number of containers she will need.

If there’s no way to distribute the liquid as described above, return -1 instead.

Example

• For totalAmount = 18 and containers = [1, 2, 5, 10],
  the output should be
  Chemicals(totalAmount, containers) = 4.Abby has access to containers with sizes 10, 5, 2, and 1, and will use one container of each size.
• For totalAmount = 9 and containers = [1, 4, 6],
  the output should be
  Chemicals(totalAmount, containers) = 3.Abby can use two containers of size 4 and one container of size 1.

Input/Output

• [time limit] 4000ms (py)

• [input] integer totalAmountThe amount of chemicals.Guaranteed constraints:
  0 ≤ totalAmount < 5 · 104.
• [input] array.integer containersA sorted array of distinct integers, denoting the container sizes.Guaranteed constraints:
  1 ≤ containers.length ≤ 15,
  0 ≤ containers[i] ≤ 1000.
• [output] integerThe minimum number of containers needed to distribute the liquid. Return -1 if there’s no way to distribute the liquid.

The Solution:

def Chemicals(totalAmount, containers):
    totalAmount+=1
    d=[999999]*totalAmount
    d[0]=0
    for x in containers:
        if x <totalAmount:
            d[x]= 1
    for x in range(totalAmount):
        for y in containers:
            if x-y>0:
                d[x]= min(d[x],d[x-y]+1)
    if d[-1]==999999:
        return -1
    return d[-1]

The Explanation:

Knapsack Problem, you can search for this term and learn more about it. In essence, create an array d. Each element of d shows the best solution up to that index. The idea follows this:

If I can get maximum value of 90 at 10 weight, and I have an item with weight 2 and value 10, then, at the best case, I can have 100 value at 92.

Reversing this, we want to minimize our weight at a given value. And slightly modifying the problem, we want to minimize number of containers at a given value.

If I can use minimum 5 containers to store 90, and I have containers of size 5, then I can have minimum 6 containers for size 95.